OLá pessoal, boa noite!!!
Estou deixando algumas aplicações para serem entregues como nossa recuperação do 4° bimestre para segunda-feira 13/12/2010.

Como podem observar todos já contém as respostas, ou seja, cabe a você aluno justificar as respostas com os devidos cálculos ou procedimentos.

:::::::::::::::::::Segue exercícios::::::::::::::::

01. (FUVEST) Considere todas as trinta e duas seqüências, com cinco elementos cada uma, que podem ser formadas com os algarismos 0 e 1. Quantas dessas seqüências possuem pelo menos três zeros em posições consecutivas?

      a) 3

      b) 5

      c) 8

      d) 12

      e) 16

RESPOSTA: C

02. (VUNESP) De uma  urna contendo 10 bolas coloridas, sendo 4 brancas, 3 pretas, 2 vermelhas e 1 verde, retiram-se, de uma vez, 4 bolas. Quantos são os casos possíveis em que aparecem exatamente uma bola de cada cor?

      a) 120

      b) 72

      c) 24

      d) 18

      e) 12

RESPOSTA: C

03. (MACK) Cada um dos círculos da figura ao lado deverá ser pintado com uma única cor, escolhida dentre quatro disponíveis. Sabendo-se que dois círculos consecutivos nunca serão pintados com a mesma cor, então o número de formas de se pintar os círculos é:

                                                                 

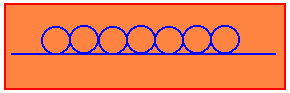
a) 100

b) 240

c) 729

d) 2916

e) 5040

RESPOSTA: D

04. (UEL) Um professor de Matemática comprou dois livros para premiar dois alunos de uma classe de 42 alunos. Como são dois livros diferentes, de quantos modos distintos pode ocorrer a premiação?

      a) 861

      b) 1722

      c) 1764

      d) 3444

      e) 2⁴²

RESPOSTA: B

05. (UNIV. EST. DE FEIRA DE SANTANA) O número de equipes de trabalho que poderão ser formadas num grupo de dez indivíduos, devendo cada equipe ser constituída por um coordenador, um secretário e um digitador, é:

      a) 240

      b) 360

      c) 480

      d) 600

      e) 720

RESPOSTA: E

06. (MACK) Os polígonos de k lados (k múltiplos de 3), que podemos obter com vértices nos 9 pontos da figura, são em número de:

                                               

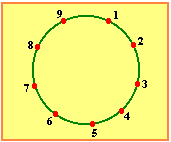
a) 83

b) 84

c) 85

d) 168

e) 169

RESPOSTA: E

07. (MACK) Um juiz dispõe de 10 pessoas, das quais somente 4 são advogados, para formar um único júri com 7 jurados. O número de formas de compor o júri, com pelo menos 1 advogado, é:

      a) 120

      b) 108

      c) 160

      d) 140

      e) 128

RESPOSTA: A

08. Do cardápio de uma festa constavam dez diferentes tipos de salgadinhos dos quais só quatro seriam servidos quentes. O garçom encarregado de arrumar a travessa e servi-la foi instruído para que a mesma contivesse sempre só 2 diferentes tipos de salgadinhos frios, e só 2 diferentes dos quentes. De quantos modos diferentes, teve o garçom a liberdade de selecionar os salgadinhos para compor a travessa, respeitando as instruções?

      a) 90

      b) 21

      c) 240

      d) 38

      e) 80

RESPOSTA: A

09. (ITA) O número de soluções inteiras, maiores ou iguais a zero, da equação x + y + z + w = 5 é:

      a) 36

      b) 48

      c) 52

      d) 54

      e) 56

RESPOSTA: E

10. (MACK) Dentre os anagramas distintos que podemos formar com n letras, das quais duas são iguais, 120 apresentam estas duas letras iguais juntas. O valor de n é:

      a) 4

      b) 5

      c) 6

      d) 7

      c) 122

RESPOSTA: C

Anagrama

O anagrama é um jogo de palavras que utiliza a transposição ou rearranjo de letras de uma palavra ou frase, com o intuito de formar outras palavras com ou sem sentido. É calculado através da propriedade fundamental da contagem, utilizando o fatorial de um número de acordo com as condições impostas pelo problema. 

Situação 01 

Vamos determinar os anagramas da palavra: 

a) ESCOLA 
A palavra possui 6 letras, dessa forma, basta determinarmos o valor de 6! (seis fatorial). 
6! = 6 * 5 * 4 * 3 * 2 * 1 = 720 

b) ESCOLA que inicia com E e termina com A. 
E ___ ___ ___ ___ A 
Vamos permutar as 4 letras não fixas. 
4! = 4 * 3 * 2 * 1 = 24 


Situação 02
a) Determinar os anagramas da palavra REPÚBLICA. 
A palavra possui 9 letras, então devemos calcular 9!. 
9! = 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 362.880 

b) REPÚBLICA que inicia com R e termina com A. 
R ___ ___ ___ ___ ___ ___ ___ A 
Vamos permutar as 7 letras não fixadas. 
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040 


Situação 03

Determinar os anagramas da palavra CONQUISTA, que tem as letras CON juntas e na mesma ordem: C O N ___ ___ ___ ___ ___ ___ . 
Temos 6 letras não fixadas que permutarão entre si, e a expressão CON que se unirá às permutações. 
7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040 


Situação 04 

A palavra MATEMÁTICA é formada por 10 letras. Determine o número possível de anagramas dessa palavra. 
Temos 10 letras que serão permutadas entre si, portanto: 

10! = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 3.628.800 

A palavra MATEMÁTICA possui 3.628.800 anagramas. 

Situação 05

Quantas palavras de 3 letras podemos formar com as letras O, L e A? Quais são essas palavras? As palavras não precisam necessariamente terem siginificado. 

A quantidade de palavras será dada por 3! 
3 * 2 * 1 = 6 palavras 

As palavras são: 

OLA 
OAL 
ALO 
AOL 
LOA 
LAO

Prof. Reinaldo Simonelli

Análise Combinatória

Análise combinatória é um estudo realizado na matemática e na lógica, é responsável  pela análise das possibilidades e das combinações. Observe alguns exemplos de exercícios que são resolvidos utilizando análise combinatória. 
Se quiserem saber quantos números de quatro algarismos são formados com os algarismos 1, 2, 3, 4, 5, 6, 7 e 9, é preciso aplicar as propriedades da análise combinatória. 

Um homem possui cinco camisas, quatro calças, três paletós e dois pares de sapatos. De quantos modos diferentes pode se vestir? Para saber essas combinações é necessário utilizar as propriedades da análise combinatória. 

Para efetuar os cálculos desses problemas devemos estudar algumas propriedades da análise combinatória: 

- Princípio fundamental da contagem;
- Fatorial;
- Arranjos simples;
- Permutação simples;
- Combinação;
- Permutação com elementos repetidos.

A análise combinatória é um dos tópicos que a matemática é dividida, responsável pelo estudo de critérios para a representação da quantidade de possibilidades de acontecer um agrupamento sem que seja preciso desenvolvê-los. 
Veja um exemplo de um problema de análise combinatória e como montamos os seus agrupamentos. 

Dado o conjunto B dos algarismos B = { 1,2,3,4}. Qual a quantidade de números naturais de 3 algarismos que podemos formar utilizando os elementos do grupo B? 

Esse é um tipo de problema de análise combinatória, pois teremos que formar agrupamentos, nesse caso formar números de 3 algarismos, ou seja, formar agrupamentos com os elementos do conjunto B tomados de 3 em 3. 

Veja como resolveríamos esse problema sem a utilização de critérios ou fórmulas que o estudo da análise combinatória pode nos fornecer. 

Esse esquema construído acima representa todos os números naturais de 3 algarismos que podemos formar com os algarismos 1,2,3,4, portanto, concluindo que é possível formar 24 agrupamentos. 

Para descobrir essa quantidade de agrupamentos possíveis não é necessário montar todo esse esquema, basta utilizar do estudo da análise combinatória que divide os agrupamentos em Arranjos simples, Combinações simples, Permutações simples e Permutações com elementos repetidos. Cada uma dessas divisões possui uma fórmula e uma maneira diferente de identificação, que iremos estudar nessa seção. 

O estudo da análise combinatória é dividido em: 

Princípio fundamental da contagem 

Fatorial 

Arranjos Simples 

Permutação Simples 

Combinação Simples 

Permutação com elementos repetidos.

Prof. Reinaldo Simonelli

Boas Vindas

Olá Pessoal!!!
Muito obrigado pela sua visita, saiba que ela é muito importante para todos nós. Neste espaço conto com sua colaboração para que possamos fazer deste blog, um ambiente elegante, agradável e acima de tudo que ns permita a reflexão e consequentemente um aprendizado matemático.
Abraços
Prof. Reinaldo Simonelli